Шек
| Бұл мақаланы Уикипедия сапа талаптарына лайықты болуы үшін уикилендіру қажет. |
Шек - математиканың негізгі ұғымдарының бірі.
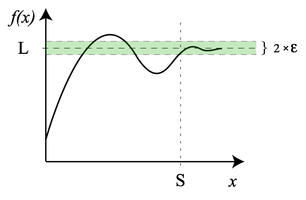
- Егер алдын ала берілген кез келген ε>0 саны үшін х айнымалы шамасының белгілі бір мәнінен бастап келесі барлық мәндері |х–а|<ε теңсіздігін қанағаттандырса, онда а саны х айнымалы шамасының шегі (ол lіmx=а немесе х→а деп белгіленеді) деп аталады.
- Егер кез келген ε>0 аз саны үшін әрқашанда N нөмірі табылып және n>N теңсіздігін қанағаттандыратын n-нің барлық мәндері үшін |xn-a|<ε теңсіздігі орындалса, онда а саны айнымалы хn тізбегінің шегі (ол не n → болғанда xn→a деп белгіленеді) деп аталады.
- Егер кез келген ε>0 аз саны үшін δ>0 саны табылып, х айнымалы шамасының |х–х0|<δ теңсіздігін қанағаттандыратын барлық мәндері үшін |f(х)–А|<ε теңсіздігі орындалса, онда А тұрақты саны f(х) функциясының х=х0 нүктесіндегі шегі (ол деп белгіленеді) делінеді.
Шектердің қазіргі теориясы 19 ғ-дың басында қалыптаса бастады. Шек ұғымы алғаш рет О.Коши еңбектерінде қолданылды. Тізбек пен функция шектерінің теориясы Б.Больцано мен К.Вейерштрасстың еңбектері негізінде қалыптасты.
Жинақтылық, математикада — белгілі бір математикалық объектінің шегі болатындығын көрсететін математикалық талдаудың негізгі ұғымдарының бірі. Осы мағынада тізбектің жинақтылықтығы, қатардың жинақтылықтығы, шексіз көбейтіндінің жинақтылықтығы, үздіксіз бөлшектің жинақтылықтығы, интегралдық жинақтылық, т.б. жөнінде айтуға болады.
a1, a2, ... нақты сандар тізбегінің жинақтылықтығы оның шекті шегі болатындығын көрсетеді: L оның шегі болса:
деп жазылып
- "an тізбегі n шексіздікке ұмтылғанда L-ге тең" деп оқылады. Қандай да бір математикалық объектінің жинақтылық қасиеті математиканың теориялық мәселелері мен математика қолданылатын жерлерде елеулі рөл атқарады.
Қатарлар мен интегралдар теориясында абсолют жинақтылық ұғымының маңызы зор. Жинақтылық ұғымы әр түрлі теңдеулерді (алгебралық, дифференциалдық, интегралдық) шешуде (Мысалы, теңдеулердің сандық шешімдерін табу кезінде) үлкен рөл атқарады.
Тарихы[өңдеу | қайнарын өңдеу]
Ежелгі дәуір математиктері (Евклид, Архимед) аудандар мен көлемдерді табу үшін шын мәніндегі шексіз қатарларды пайдаланған. “Жинақтылық” терминін шотланд математигі және астрономы Дж. Грегори (1638 — 1675) қатарлар үшін қолданды (1668). XVII ғасырда жинақтылық ұғымы шашыраңқы қатарларды талдауда кеңінен қолданыла бастады (Л.Эйлер). Қатарлардың жинақтылықтығын зерттеудің дәлірек әдістері 19 ғ-да жасалды (О.Коши, Н.Абель, Б.Больцано, К.Вейерштрасс, т.б.). Бірқалыпты Жинақтылық ұғымы Н.Абельдің (1826), Ф.Зейдельдің (1847 — 48) және Дж. Стокстің (1848) еңбектерінде тұжырымдалды. Функциялар теориясының, функционалдық анализдің және топологияның дамуына байланысты жинақтылық ұғымы одан әрі кеңейтілді.
Дереккөздер[өңдеу | қайнарын өңдеу]
| Өтініш, осы бөлімді толықтырыңыз. |
- Қазақ энциклопедиясы, 9 том