Лиссажу пішіндері
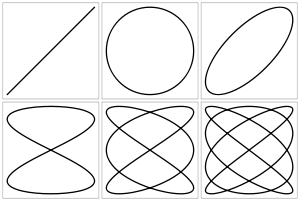
Лиссажу пішіндері (Лиссажу фигуралары) — жиілігі рационал қатынастағы өзара перпендикуляр тербелістер жасайтын нүктелердің траекториясы.[1] Алғаш рет француз ғалымы Жюль Антуан Лиссажу зерттеген. Пішін түрі екі тербелістің периодтарының, жиіліктерінің, фазаларының және амплитудаларының қатынастарына тәуелді болып келеді. Қалыпты жағдайда екі тербелістің периодтары тең болғанда кезде тербеліс пішіні эллипс болып келеді. Фазалар айырымы 0 немесе болған кезде пішін түзу кесіндісі түрінде болады, ал егер фазалар айырымы және амплитудалары тең болса тербеліс пішіні шеңбер болады. Егер екі тербелістің периодтары сәйкес келмесе, онда фазалар айырымы үнемі өзгеріп тұрады, нәтижесінде эллипс үнемі деформацияға ұшырайды. Периодтарды айырмашылығы елеулі болған кезде Лиссажу пішіндері байқалмайды. Алайда, егер периодтар бүтін сандық еселік қатыста болса, екі периодтың еселіктерінің ең аз дегендегі уақыт аралығында қозғалушы нүкте бастапқы орнына қайтып келеді. Бұл жағдайда күрделі формадағы Лиссажу пішіндері пайда болады. Лиссажу пішіндері төртбұрыштарға салынады, бұл төртбұрыштың ортасы координаталар басымен сәйкес келеді, ал қабырғалары координаталар осьтеріне параллель және екі шетінен де тербеліс амплитудасының шамасына тең қашықтықта орналасады.
Лиссажу қисығының математикалық көрінісі[өңдеу | қайнарын өңдеу]
мұндағы A, B — тербелістердің амплитудалары, a, b — жиіліктер, δ — фазалар ығысуы
Қисықтың түрі a/b қатынасына тәуелді. Қатынас 1-ге тең болғанда, Лиссажу пішіні эллипс тұрпатты болады,белгілі бір жағдайларда ол шеңбер (A = B, δ = π/2 радиан) және түзу кесіндісі (δ = 0) түрінде болады. Лиссажу пішінінің тағы бір мысалы - парабола (a/b = 2, δ = π/2). Басқа қатынастар кезінде Лиссажу пішіндері тұйықталған күрделі пішін болып келеді, бұл кезде a/b қатыснасының рационал сан болуы шарты орындалу керек.
a = 1, b = N (N — натурал сан) және
кезіндегі Лиссажу пішіндері N дәрежесінің бірінші текті Чебышёв көпмүшелігі болып табылады.
Мысалдар[өңдеу | қайнарын өңдеу]
Төменде берілген анимация қатынасының 0.01 қадамымен 0-ден 1-ге дейін артқандағы қисықтардың өзгерісін көрсетеді.(δ=0)
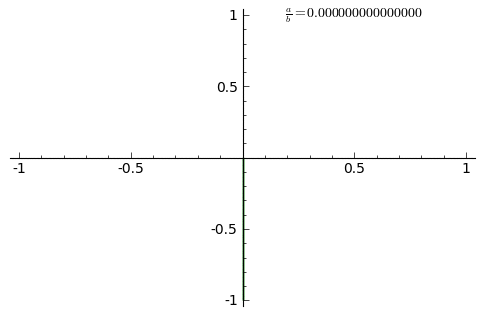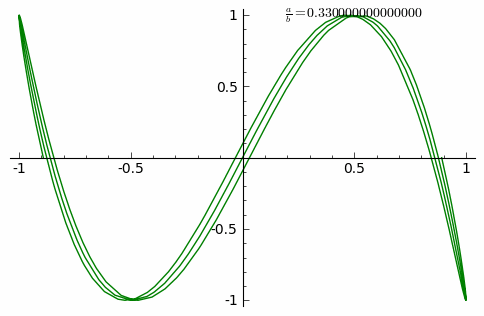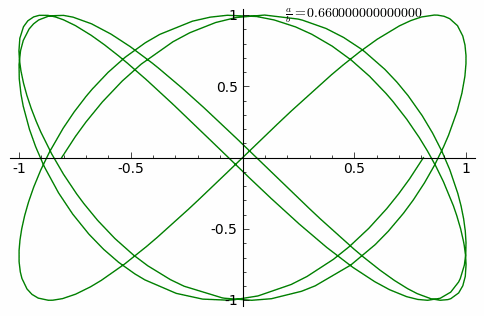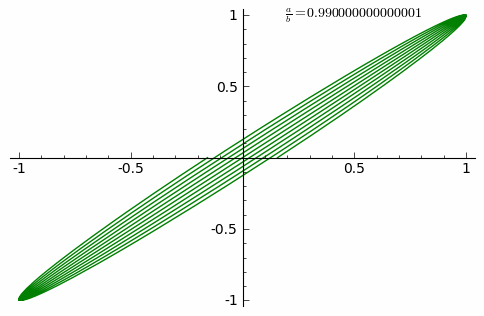
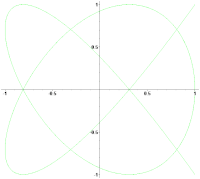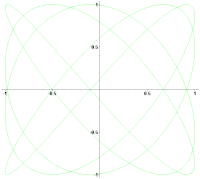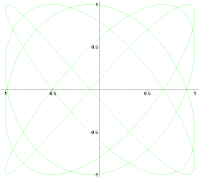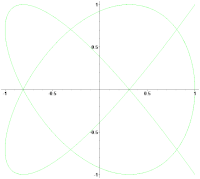
Төменде δ = π/2, a тақ натурал сан және b натурал сан және |a − b| = 1 жағдайындағы Лиссажу пішіндері келтірілген.
-
a = 1, b = 2 (1:2)
-
a = 3, b = 2 (3:2)
-
a = 3, b = 4 (3:4)
-
a = 5, b = 4 (5:4)
-
a = 5, b = 6 (5:6)
-
a = 9, b = 8 (9:8)
Техникада қолданылуы — жиіліктерді салыстыру[өңдеу | қайнарын өңдеу]

Егер осциллографтың «X» және «Y» кірістеріне жақын жиіліктердің сигналдарын қоссақ, Лиссажу пішіндерін көруге болады. Бұл әдіс екі сигнал көздерінің жиіліктерін салыстыру және бір көздің жиілігін екіншісіне сәйкестендіріп баптау үшін қолданылады. Жиіліктер мәндері жақын, бірақ тең емес болғанда экрандағы фигура айналады. Бұл кезде айналым циклының периоды жиіліктер айырымның мәніне қарама-қарсы болады, мысалы, айналым периоды 2 с болса, жиіліктер айырымы 0,5 Гц болады. Жиіліктер тең болған кезде пішін кез келген фазада тыныштықта тұрады, алайда іс жүзінде аз уақытты сигналдардың тұрақсызыдығы нәтижесінде осциллограф экрандағы пішін сәл дірілдеп тұрады. Салытыруға тек ұқсас жиіліктерді емес, сонымен қатар еселік қатынастағы жиіліктерді де пайдаланса болады, мысалы, егер дұрысталған үлгіде жиілік 5 МГц, ал бапталып жатқан үлгіде 2,5 МГц болса.
Дереккөздер[өңдеу | қайнарын өңдеу]
- ↑ Орысша-қазақша түсіндірме сөздік: Физика / Жалпы редакциясын басқарған э.ғ.д,, профессор Е. Арын – Павлодар: С. Торайғыров атындағы Павлодар мемлекеттік университеті, 2006. ISBN 9965-808-88-0
- Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978
- Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981
Сілтемелер[өңдеу | қайнарын өңдеу]
- Лиссажу пішіндерін онлайн тұрғызу Мұрағатталған 15 сәуірдің 2008 жылы.
- Circuits. Over Passive Circuits. Lissajous Figures
| Бұл мақаланы Уикипедия сапа талаптарына лайықты болуы үшін уикилендіру қажет. |










