Менелай теоремасы

Менела́й теоре́масы немесе трансверсалдар туралы теорема немесе толық төртқабырғалық туралы теорема — бұл аффиндік геометрияның классикалық теоремасы.

Тұжырымдамасы

Сурет:Teorema menelaya.gif

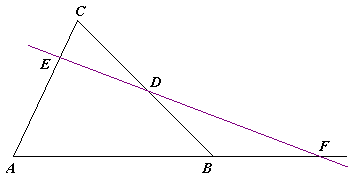
Егер $A',B'$ және $C'$ нүктелері сәйкесінше $\triangle ABC$ үшбұрышының $BC,CA$ және $AB$ қабырғаларында немесе олардың созындыларында жатса ^[1], онда олар коллинеар болады сонда тек сонда, егер

$\frac{AB'}{B'C}\cdot\frac{CA'}{A'B}\cdot\frac{BC'}{C'A}=-1.$

мұндағы $\frac{AB'}{B'C}$, $\frac{CA'}{A'B}$ және $\frac{BC'}{C'A}$ бағытталған кесінділер қатынасын белгілейді,.

Бұл теоремадан мынадай қатынас шығады:

$\frac{|AB'|}{|B'C|}\cdot\frac{|CA'|}{|A'B|}\cdot\frac{|BC'|}{|C'A|}=1.$

Дәлелдеу  

С нүктесі арқылы AB-ға параллель түзу жүргізейік, K деп осы түзудің A'C' -мен қиылысу нүктесін белгілейік. Үшбұрыштар $\triangle AC'B'$ мен $\triangle CKB'$ ұқсас болғандықтан (екі бұрыштары бойынша), онда

$\frac{|AC'|}{|CK|} = \frac{|B'A|}{|B'C|}$.

Сонымен қатар $\triangle BC'A'$ мен $\triangle CKA'$ үшбұрыштары да ұқсас болғандықтан

$\frac{|CK|}{|C'B|} = \frac{|A'C|}{|BA'|}$.

CK-ны алмастыру арқылы табатынымыз

$\frac{|AC'|}{|C'B|}\cdot\frac{|BA'|}{|A'C|}\cdot\frac{|CB'|}{|B'A|} = 1$.

$A',B'$ мен $C'$ нүктелерінің екі түрлі орналасуы бар: екеуі сәйкес қабырғаларында, ал үшіншісі үшінші қабырға созындысында немесе үшеуі де үш сәйкес қабырға созындыларында жатуы мүмкін. Осыдан бағытталған кесінділер қатынасы үшін шығатыны

$\frac{AB'}{B'C}\cdot\frac{CA'}{A'B}\cdot\frac{BC'}{C'A}=-1.$

Вариациялары мен жалпыламалары

• Тригонометриялық баламасы:

$\frac{\sin\angle BAA'}{\sin\angle A'AC} \cdot \frac{\sin\angle CBB'}{\sin\angle B'BA} \cdot \frac{\sin\angle ACC'}{\sin\angle C'CB}=-1$, мұндағы барлық бұрыштар — бағдарланған.

• Сфералық геометрияда Менелай теоремасы былай түрленеді

$\frac{\sin |AB'|}{\sin |B'C|}\cdot\frac{\sin |CA'|}{\sin |A'B|}\cdot\frac{\sin |BC'|}{\sin |C'A|} = 1.$

• Лобачевский геометриясында Менелай теоремасы түрі

$\frac{\operatorname{sh} |AB'|}{\operatorname{sh} |B'C|}\cdot\frac{\operatorname{sh} |CA'|}{\operatorname{sh} |A'B|}\cdot\frac{\operatorname{sh} |BC'|}{\operatorname{sh} |C'A|} = 1.$

Тарихы

Бұл теорема Алесандриялық Менелайдың «Сферикасының» үшінші бөлімінде (шамамен БД 100 ж.) дәлелдейді. Ол басында теореманың жазық нұсқасын дәлелдейді, содан орталық проекциялаумен сфераға көшіреді. Жазықтықтағы нұсқасы оныі алдында сақлмаған Еуклидтің «Поризмаларында» дәлелденуі мүмкін.

Қолданысы

• Салмон теоремасы

тағы қараңыз

• Гаусс түзуі
• Чева теоремасы

Сілтемелер

• Үлгі қатесі: қара {{Кітап}}
• Үлгі:Книга:Коксетер. Грейтцер. Новые встречи с геометрией
• Үлгі:Книга:Элементарная геометрия. Понарин
• Үлгі қатесі: қара {{Мақала}}
• Үлгі қатесі: қара {{Мақала}}