Логарифм
Логарифм (logos — қатынас және arіthmos — сан), N санының негізі бойынша логарифмі — N санын алу үшін а саны дәрежеленетін m дәреже көрсеткіші (Логарифм негізі), бұл түрінде белгіленеді. Сонымен, егер болса, . болғанда шексіз көп оң сандардың нақты логарифмі болмас еді, сондықтан да деп алынады. Логарифмдік функциялардың қасиеті бойынша, кез келген оң санның берілген негізі бойынша бір ғана нақты Логарифмі болады (теріс санның Логарифмі комплекс сан).
Логарифмнің негізгі қасиеттері:
Егер a негізі белгілі болса, анықталған Логарифм жүйесі туралы айтуға болады. Әдетте түрінде белгіленетін ондық Логарифм () көбірек қолданылады. 10k (k — бүтін сан) санынан басқа рационал санның ондық Логарифмі ондық бөлшек түрінде жуықтап өрнектелетін трансцендент сан. Ондық Логарифмнің бүтін бөлігін сипаттамасы, ал бөлшек бөлігін мантиссасы деп атайды. болғандықтан, 10k көбейткішімен ерекшеленетін сандардың ондық Логарифмінің мантиссасы бірдей, тек сипаттамалары әр түрлі болады. Логарифм кестелері осы қасиетке негізделіп жасалған, онда бүтін сандардың тек мантиссалары ғана берілген. Негізі трансцендент сан болатын натурал Логарифмнің де маңызы зор; ол түрінде белгіленеді. Логарифмнің бір негізінен екінші негізіне ауысу үшін формуласы қолданылады. көбейткіші a негізден b негізге ауысу (өту) модулі деп аталады. Натурал Логарифмнен ондық Логарифмге немесе керісінше өту
формулалары арқылы жүзеге асырылады.
Логарифм атауын Дж. Непер ұсынған. Логарифм ең алдымен 16 ғасырда астрономияның тез дамуымен, астрономия бақылауларды анықтай түсуге және астрономия есептеулердің күрделілене түсуіне байланысты ашылды. Алғашқы Логарифм кестелерінің авторлары геометриялық прогрессия қасиеттері мен оның мүшелерінің дәреже көрсеткіштерінен құрастырылған арифметикалық прогрессия қасиеттерінің арасындағы тәуелділікті пайдаланған. Бұл тәуелділіктерді б.з.б. 3 ғасырда Архимед ішінара байқаған болатын, 1484 ж. Н.Шюке, 1544 ж. М.Штифель оларды жақсы білген. Алғашқы Логарифм кестелерін 1614 — 1619 ж. Дж.Непер мен 1620 ж. Й.Бюрги бір-біріне тәуелсіз және бір мезгілде құрастырған. Логарифмді теория тұрғыдан зерттеуде Бельгия математигі Григорий мен Л.Эйлер (1707 —1783) еңбектерінің маңызы зор.

Логарифмдік функция[өңдеу | қайнарын өңдеу]
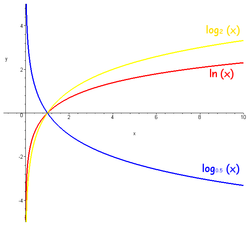
Логарифмдік функция — көрсеткіштік функциясына кері функциясы. х аргументінің белгілі бір мәніне сәйкес келетін у Логарифмдік функцияның мәні х санының натурал логарифмі деп аталады. Логарифмдік функцияның негізгі қасиеттері көрсеткіштік функция мен логарифмдердің қасиеттерінен шығады. Математика анализ курсында (мұндағы , , ) Логарифмдік функциясы қарастырылады. Бұл функция Логарифмдік функциямен қатынасы арқылы байланысады. Логарифмдік функциясы x>0 болғанда анықталған, бірсарынды (монотонды) ( болғанда өседі, болғанда кемиді), үзіліссіз және шексіз дифференциалданады. Логарифмдік функция өзінің анықталу облысындағы әрбір нүктенің маңайында дәрежелік қатарға жіктелуі мүмкін.
Қарапайым логарифмдік теңдеу және теңсіздіктің мәндес өзгерісінің орындалу схемасы[өңдеу | қайнарын өңдеу]
( болғандықтан, онда және сондықтан ақырғы теңдеудің (ММЖ) (ОДЗ) автоматты түрде ескеріледі.)
немесе
- , мұнда
онда Теңсіздің таңбасы өзгермейді және (ММЖ) (ОДЗ) есептеледі
онда Теңсіздің таңбасы өзгереді және (ММЖ) (ОДЗ) есептеледі








































